冒泡排序及其变种
# 冒泡排序
# 介绍
冒泡排序,是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。每次冒泡,都会将最大的数移动到最末端,并缩小冒泡范围。
# 动画
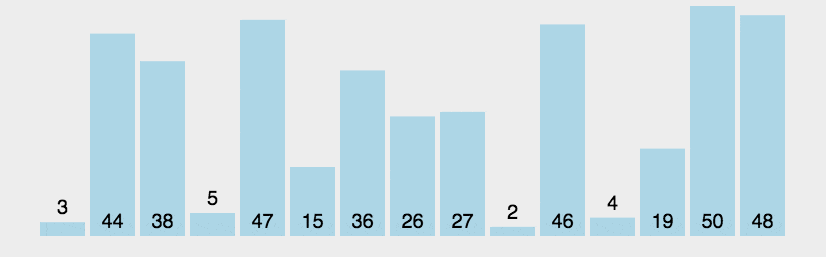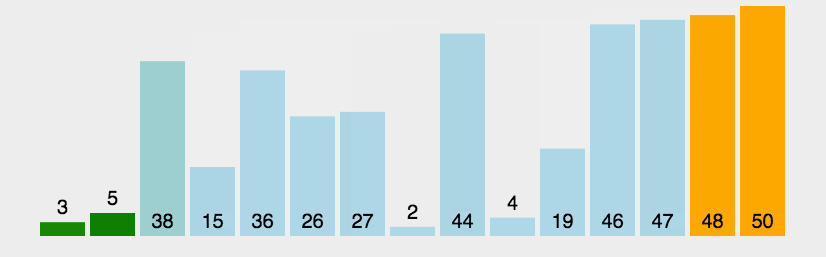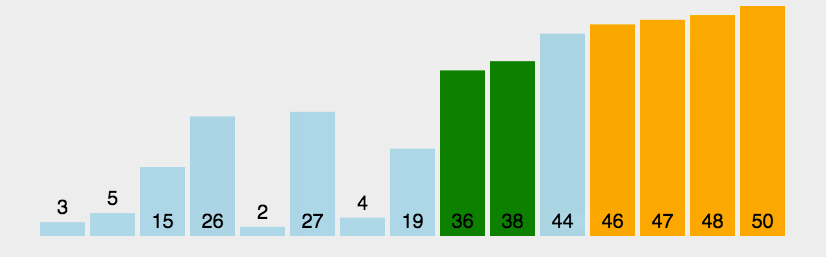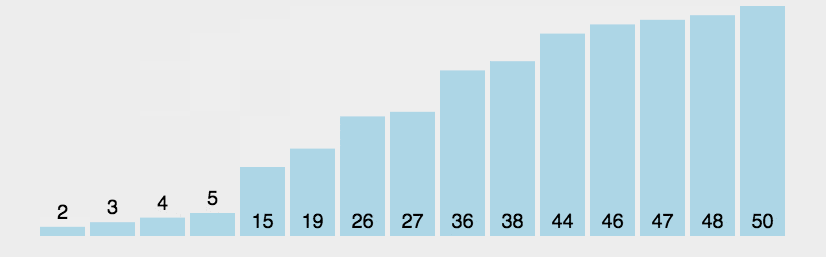
# 代码示例
void bubbleSort(vector<int>& vec) { | |
for(int i = 0; i < vec.size() - 1; i++) { | |
bool swapFlag = false; | |
for(int j = 0; j < vec.size() - 1 - i; j++) { | |
if(vec[j] > vec[j+1]) { | |
swap(vec[j], vec[j + 1]); | |
swapFlag = true; | |
} | |
} | |
if(!swapFlag) break; | |
} | |
} |
# 鸡尾酒排序
# 介绍
鸡尾酒排序,是冒泡排序的轻微变形。不同的地方在于从低到高然后从高到低,而冒泡排序则仅从低到高去比较序列里的每个元素。他可以得到比冒泡排序稍微好一点的性能,原因是冒泡排序只从一个方向进行比对(由低到高),每次循环只移动一个项目。鸡尾酒排序,对于乌龟(序列末端较小的数)比较多的情况,相对于原始冒泡排序有更好的性能。
以序列(2,3,4,5,1)为例,鸡尾酒排序只需要访问一次(来回两趟)序列就可以完成排序,但如果使用冒泡排序则需要四次。
# 动画
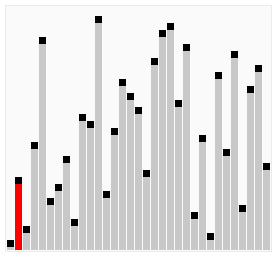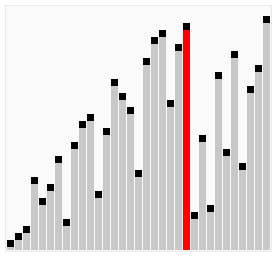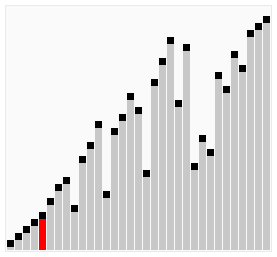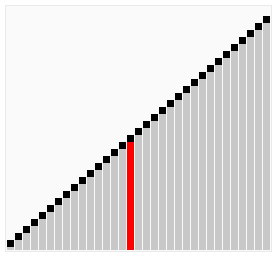
# 代码示例
void cocktailSort(vector<int>& vec) { | |
int left = 0; | |
int right = vec.size() - 1; | |
while(left < right) { | |
bool swapFlag = false; | |
for(int i = left; i < right; i++) { | |
if(vec[i] > vec[i + 1]) { | |
swap(vec[i], vec[i + 1]); | |
swapFlag = true; | |
} | |
} | |
right--; | |
for(int i = right; i > left; i--) { | |
if(vec[i - 1] > vec[i]) { | |
swap(vec[i], vec[i - 1]); | |
swapFlag = true; | |
} | |
} | |
left++; | |
if(!swapFlag) break; | |
} | |
} |
# 梳子排序
# 介绍
梳子排序,改良自冒泡排序和快速排序,其要旨在于消除乌龟,亦即在数组尾部的小数值,这些数值是造成冒泡排序缓慢的主因。相对地,兔子,亦即在数组前端的大数值,不影响冒泡排序的性能。
在冒泡排序中,只比较数组中相邻的二项,即比较的二项的间距(Gap)是 1,梳排序提出此间距其实可大于 1,改自插入排序的希尔排序同样提出相同观点。梳排序中,开始时的间距设置为数组长度,并在循环中以固定比率递减,通常递减率设置为 1.3(约为原 gap 的 1/8)。在一次循环中,梳排序如同冒泡排序一样把数组从首到尾扫描一次,比较及交换两项,不同的是两项的间距不固定于 1。如果间距递减至 1,梳排序假定输入数组大致排序好,并以冒泡排序作最后检查及修正。
在 gap 大于 1 时,每次将 gap 递减并执行一次冒泡过程,在 gap 变到 1 时,执行正常的冒泡排序,但是由于前面的梳理,只需要极少量的冒泡就能得到有序的数组。
# 动画
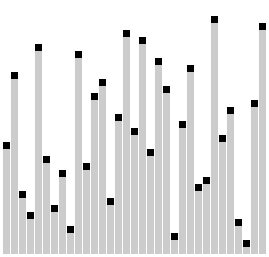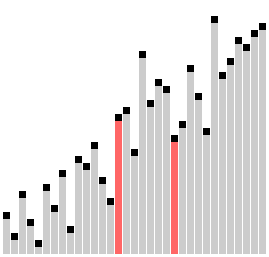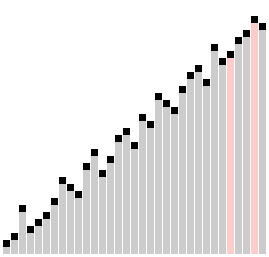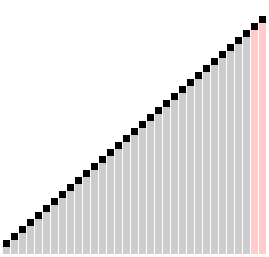
# 代码示例
void combSort(vector<int>& vec) { | |
int gap = vec.size(); | |
bool swapFlag = true; | |
while(gap > 1 || swapFlag) { | |
if (gap > 1) { | |
gap = int (gap * 0.8); | |
} | |
swapFlag = false; | |
for (int i = 0; gap + i < vec.size(); i++) { | |
if (vec[i] > vec[i + gap]) { | |
swap(vec[i], vec[i + gap]); | |
swapFlag = true; | |
} | |
} | |
} | |
} |
# 递减率
递减率的设置影响着梳排序的效率,原作者以随机数作实验,得到最有效递减率为 1.3 的。如果此比率太小,则导致一循环中有过多的比较,如果比率太大,则未能有效消除数组中的乌龟。
亦有人提议用! 作递减率,同时增加换算表协助于每一循环开始时计算新间距。
因为编程语言中乘法比除法快,故会取递减率倒数与间距相乘,
# 其它优化
设置递减率为 1.3 时,最后只会有三种不同的间距组合:(9, 6, 4, 3, 2, 1)、(10, 7, 5, 3, 2, 1)、或 (11, 8, 6, 4, 3, 2, 1)。实验证明,如果间距变成 9 或 10 时一律改作 11,则对效率有明显改善,原因是如果间距曾经是 9 或 10,则到间距变成 1 时,数值通常不是递增序列,故此要进行几次冒泡排序循环修正。加入此指定间距的变异形式称为梳排序 - 11
# bilibili 视频分享
# 总结
冒泡排序、鸡尾酒排序、梳排序都是优美的算法,后两种属于第一种的优化,但是冒泡排序只适合处理序列大致有序的情况,对于绝大多数的一般序列远不如归并排序、快速排序等算法。也不会有任何语言将冒泡排序作为默认的排序算法,他们大都选择快速排序 + 插入排序的组合算法。
